Project Euler

最近在刷Project Euler的题目, 非常有意思, 都是一些有着简短描述的数学题目, 而且提交答案只需要最终结果, 所以不限语言, 不限方法, 尤其适合对数学和编程感兴趣的人。对它不了解的人可以在维基的这个页面查看相关介绍, 而且国内已经有人做了一个中文翻译站, 有时间的时候刷一刷还挺有意思的。

第15题

进展一直很顺利, 但是到第15题的时候发现提交答案的人数一下少了很多, 心想看来这道题目有点难度啊。尝试了一下, 第一次的算法可行, 但是经过测算需要几千小时。。。。。。继续改进, 还是太慢, 最后, 终于达到了毫秒级别！所以就感觉这个思考的过程还是挺有意思的。 从一个2×2网格的左上角开始, 有6条（不允许往回走）通往右下角的路。

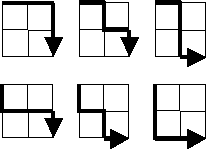
对于20×20的网格, 这样的路有多少条？

思路过程

路径查找

1
2
3

0,0  0,1  0,2
1,0  1,1  1,2
2,0  2,1  2,2

第一条路径

首先结合上面的图观察它的坐标变化： 从起始点(0,0)开始, 向右有(0,1)和向下有(1,0), 两个方向都可以; 而图中第一条路径选择向右, 因此我们可以记录路径为(0,0) → (0,1), 可选的坐标列表为(1,0); 此时向右有(0,2)和向下有(1,1), 两个方向都可以; 结合图中的第一条路径, 我们还是选择向右, 因此记录路径为(0,0) → (0,1) → (0,2), 可选的坐标列表变为(1,0), (1,1); 此时向右没有坐标, 向下有(1,2), 和图中第一条路径相符, 因此记录路径为(0,0) → (0,1) → (0,2) → (1,2); 同上, 向右没有坐标, 向下有(2,2), 和图中第一条路径相符, 因此记录路径为(0,0) → (0,1) → (0,2) → (1,2) → (2,2);

第二条路径

很明显, 对于(1,2)和(2,2)都是因为向下没有坐标了, 因此要寻找新的路线肯定要回退到有两个方向可选的那个坐标, 然后再继续这个过程。 第一条路径为(0,0) → (0,1) → (0,2) → (1,2) → (2,2), 记录下来的可选坐标列表为(1,0), (1,1); 路径中最后一个出现两个方向的坐标为(0,1), 因此需要回退到这里, 路径变为(0,0) → (0,1); 从可选坐标列表中取出最后一个坐标作为新的方向, 路径变为(0,0) → (0,1) → (1,1), 可选的坐标列表为(1,0); 此时向下有(2,1), 则可选的坐标列表变为(1,0), (2,1), 向右有(1,2), 则路径变为(0,0) → (0,1) → (1,1) → (1,2); 向右没有坐标, 向下有(2,2), 和图中第二条路径相符, 因此记录路径为(0,0) → (0,1) → (1,1) → (1,2) → (2,2);

第三条路径

同样的回退策略, 回退到坐标(1,1), 再使用同样的前进策略, 得到路径(0,0) → (0,1) → (1,1) → (2,1) → (2,2)

第四、五、六条路径

同样的回退和前进策略, 即可得到第四、五、六条路径

代码实现

根据以上的前进、回退策略, 结合栈即可实现如下的代码

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59

def path_count(n, m):
    # 用于记录路径
    stack = []

    # 用于记录出现分支时向下的点坐标
    temp = []

    # 坐标值和路径次数
    i = 0; j = 0

    # 用于记录路径次数
    count = 0

    # 将起始点(0, 0)放入路径中
    stack.append((i, j))

    while len(stack) > 0:
        # 为路径中的最后一个点查找下一个点
        (i, j) = stack[-1]

        # 是否可以继续向下
        if i+1 <= n:
            # 是否可以继续向右
            if j+1 <= m:
                # 出现分支时将向下的点坐标存入temp以备回退, 向右的点坐标存入stack作为路径
                temp.append((i+1, j))
                stack.append((i, j+1))
            else:
                # 只能向下则直接将向下的点坐标存入路径
                stack.append((i+1, j))
        else:
            # 只能向右则直接将向右的点坐标存入路径
            if j+1 <= m:
                stack.append((i, j+1))

        # 路径中的最后一个点坐标是否为终点
        if stack[-1] == (n, m):
            # 此时可打印查看路径
            print stack

            # 路径次数增加
            count += 1

            # 可选的坐标列表为空时退出循环
            if len(temp) == 0:
                break

            # 回退操作
            # 取出最后一个出现分支时向下的那个点坐标
            (ti, tj) = temp.pop()

            # 依次取出路径中的坐标, 直到此坐标与(ti, tj)互为一个分支节点的向右和向下节点
            (si, sj) = stack.pop()
            while not (si+1 == ti and tj+1 == sj):
                (si, sj) = stack.pop()

            # 将最后一个出现分支时向下的那个点坐标添加到路径中
            stack.append((ti, tj))
    return count

运行以上代码即可得到如下六条2x2网格的路径

1
2
3
4
5
6

[(0, 0), (0, 1), (0, 2), (1, 2), (2, 2)]
[(0, 0), (0, 1), (1, 1), (1, 2), (2, 2)]
[(0, 0), (0, 1), (1, 1), (2, 1), (2, 2)]
[(0, 0), (1, 0), (1, 1), (1, 2), (2, 2)]
[(0, 0), (1, 0), (1, 1), (2, 1), (2, 2)]
[(0, 0), (1, 0), (2, 0), (2, 1), (2, 2)]

计算次数-递归方法

虽然以上代码可以求得nxn网格的路径, 但是换到20x20时它复杂的入栈出栈操作会拖累整个运行时间, 使用这个办法求解次数显然是不行的, 只能继续查找一些规律了。

1
2
3
4

0,0  0,1  0,2  0,3
1,0  1,1  1,2  1,3
2,0  2,1  2,2  2,3
3,0  3,1  3,2  3,3

画出一个3x3的网格来, 想着2x2的时候从起始点(0,0)出发, 首先选择向右有三条路径, 然后3*2=6, 同理, 对于3x3的网格来说, 总共有20条路径, 从起始点出发, 选择向右则有10条路径, 那么这十条路线是如何得到的呢? 从(0,0)出发, 只考虑向右的(0,1)这个方向, 因为向下向右两个方向对称, 所以20/2=10; 而对于(0,1)来说, 它也有两个方向(1,1)和(0,2), 则可知这十条路径即为在这两个方向产生的; 对于(1,1)来说, 它到底终点(3,3)其实即为一个2x2网格, 因此这个方向有6条路径, 那么(0,2)将贡献4条路径; 经过验证, 对于3x1网格来说确实有4条路径; 由此我们即可得到: f(3, 3) = [f(2, 2) + f(3,1)]*2 进而进行推广: f(n, n) = [f(n-1, n-1) + f(n, n-2)]*2 显然, 有f(1, 1) = 2和f(n, 0) = 1 于是就可以采用递归方式来实现了

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

# 递归求解 nxm 网格的路径
def func_iter(n, m):
    if m == 0:
        return 1
    if m == 1:
        return n+1
    if n == m:
        if n == 1:
            return 2
        return (func_iter(n-1, n-1) + func_iter(n, n-2))*2
    return func_iter(n-1, m) + func_iter(n, m-1)

# 尾递归求解 nxn 网格的路径
def func(idx, count, n):
    if idx < n:
        count = (count + func_iter(idx+1, idx-1))*2
        return func(idx+1, count, n)
    return count

但是很不幸, 虽然这种实现并没用记录具体的路径, 但是递归的次数还是太多, 而且在计算n*m网格时存在太多的重复计算导致仍然会消耗比较多的时间, 因此如果能记录下已经计算出结果的n*m, 那么速度将会大大提高。

计算次数-循环方法

根据f(3, 3) = [f(2, 2) + f(3, 1)]*2, 可知问题出在f(3, 1)需要计算, 同理对于f(4, 4) = [f(3, 3) + f(4, 2)]*2, 其中f(4, 2)也需要计算, 继续按照分解f(3, 3)到f(2, 2)的过程, 可以得到: f(4, 2) = f(3, 2) + f(4, 1) f(3, 2) = f(2, 2) + f(3, 1) 于是推得公式: f(n, m) = f(n-1, m) + f(n, m-1) 根据这个公式可以发现一些比较有意思的事情, 比如当m = 1时有f(n, 1) = f(n-1, 1) + f(n, 0)， 而f(n, 0) = 1, 所以有f(n, 1) = f(n-1, 1) + 1, 同理对f(n-1, 1)展开, 得到f(n, 1) = f(n-2, 1) + 2, 这样最后将得到f(n, 1) = n+1。 同样的推理过程, f(n, 2) = f(n-1, 2) + f(n, 1)即为f(n, 2) = f(n-1, 2) + (n+1), 这样即可得知: f(n, 1)的值是一个等差数列, f(n, 2)前项减后项的值是一个等差数列, 进而推广到f(n, 3)需要做两次差才能得到等差数列。 取n = 4进行验证:

1
2
3
4
5
6
7

f(n, 0) = 1
f(1, 1) = 2    f(2, 2) = 6     f(3, 3) = 20    f(4, 4) = 70
f(2, 1) = 3    f(3, 2) = 10    f(4, 3) = 35    f(5, 4) = 126
f(3, 1) = 4    f(4, 2) = 15    f(5, 3) = 56    f(6, 4) = 210
f(4, 1) = 5    f(5, 2) = 21    f(6, 3) = 84
f(5, 1) = 6    f(6, 2) = 28
f(6, 1) = 7

对f(n, 3)进行验证, 前项减后项, 做两次即可得到等差数列, 进而即可发现: 求解f(3, 3)时, 由f(3, 3) = [f(2, 2) + f(3, 1)]*2可以得到 求解f(4, 4)时, 由f(4, 4) = [f(3, 3) + f(4, 2)]*2可以得到 因此对于f(n, n)来说, 使用公式f(n, n) = [f(n-1, n-1) + f(n, n-2)]降维后可由前面的值组合而成, 因此即可得到如下求解过程: 要求f(3, 3), 其中f(n, 0) = 1, f(n, 1) = n+1为已知项, 进而可得到如下推导过程: f(2, 2) = [f(1, 1) + f(2, 0)]*2 = (2+1)*2 = 6 f(3, 2) = f(2, 2) + f(3, 1) = 6+4 = 10 f(3, 3) = [f(2, 2) + f(3, 1)]*2 = (6+4)*2 = 20 对f(4, 4)进行验证, 仍然可以使用此方法得到正确结果, 因此对于f(n, n)可以依次求解f(n, m), m从 0 到 n来求解。

代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

def func(n):
    # 使用字典存储依次求解的f(n, m)的值, 其中f(n,1) = n+1, f(n,0) = 0记为已知项
    d = dict([((i, 1), i+1) for i in range(1, n+1) ])
    for i in range(1, n+1):
        d[(i, 0)] = 1

    # f(n, 0), f(n, 1) 已经放入字典中, 因此 m 从 2 循环到 n
    m = 2
    idx = 2
    while m <= n:
        # 对于每个 m 值, 求解f(m, m), f(m+1, m), ..., f(n, m), 因此需要使用idx记录这个变化过程
        while idx <= n:
            if idx == m:
                d[m, m] = (d[(m-1, m-1)] + d[(m, m-2)])*2
                print (m,m), (d[(m-1, m-1)] + d[(m, m-2)])*2
            else:
                d[idx, m] = d[(idx-1, m)] + d[(idx, m-1)]
            idx += 1
        m += 1
        idx = m

使用此方法求解时间即可达到毫秒级别。

终极解法

提交答案后可以查看其他人提交的解法, 这才知道原来这个问题求解的是卡塔兰数, 看题目给出的2x2网格的路径图, 从起点到终点共有四步, 这四步中必然有横着的两步和竖着的两步, 所以总路径数其实就是从四步中挑选两横两竖的组合有多少种, 因此这就转化成了一个排列组合问题! 而对于排列组合从2n中选择n个的求解有公式(2n)!/(n!)^2, 因此这个问题就可以直接套用公式来求解了！